Tag: 2019

Posted on

Relocation with Uniform External Control in Limited Directions

Title: Relocation with Uniform External Control in Limited Directions (Short Abstract)
Authors: Jose Balanza-Martinez, David Caballero, Angel A. Cantu, Timothy Gomez, Austin Luchsinger, Robert Schweller, and Tim Wylie.
Conference: The 22nd Japan Conference on Discrete and Computational Geometry, Graphs, and Games (JCDCG^3’19), 2019.

Abstract: We study a model where particles exist within a board and move single units based on uniform external forces. We investigate the complexity of deciding whether a single particle can be relocated to another position in the board, and whether a board configuration can be transformed into another configuration. We prove that the problems are NP-Complete with $1 \times 1$ particles even when only allowed to move in 2 or 3 directions.

Posted on

Discrete Planar Map Matching

Title: Discrete Planar Map Matching

Authors: Bin Fu, Robert Schweller, Tim Wylie

Conference: The 31st Canadian Conference on Computational Geometry (CCCG’19)

Abstract:

Route reconstruction is an important application for Geographic Information Systems (GIS) that rely heavily upon GPS data and other location data from IoT devices. Many of these techniques rely on geometric methods involving the Frechet distance to compare curve similarity. The goal of reconstruction, or map matching, is to find the most similar path within a given graph to a given input curve, which is often only approximate location data. This process can be approximated by sampling the curves and using the discrete Frechet distance. Due to power and coverage constraints, the GPS data itself may be sparse causing improper constraints along the edges during the reconstruction if only the continuous Frechet distance is used. Here, we look at two variations of discrete map matching: one constraining the walk length and the other limiting the number of vertices visited in the graph. We give an efficient algorithm to solve one and prove the other is NP-complete and the minimization version is APX-hard while also giving a parameterized algorithm to solve the problem.

Posted on

Covert Computation in Self-Assembled Circuits

Title: Covert Computation in Self-Assembled Circuits

Authors: Angel Cantu, Austin Luchsinger, Robert Schweller, and Tim Wylie

Conference: The 46th International Colloquium on Automata, Languages, and Programming (ICALP ’19)

Abstract:

Traditionally, computation within self-assembly models is hard to conceal because the self-assembly process generates a crystalline assembly whose computational history is inherently part of the structure itself. With no way to remove information from the computation, this computational model offers a unique problem: how can computational input and computation be hidden while still computing and reporting the final output? Designing such systems is inherently motivated by privacy concerns in biomedical computing and applications in cryptography.

In this paper we propose the problem of performing “covert computation” within tile self-assembly that seeks to design self-assembly systems that “conceal” both the input and computational history of performed computations. We achieve these results within the growth-only restricted abstract tile assembly model (aTAM) with positive and negative interactions. We show that general-case covert computation is possible by implementing a set of basic covert logic gates capable of simulating any circuit (functionally complete). To further motivate the study of covert computation, we apply our new framework to resolve an outstanding complexity question; we use our covert circuitry to show that the unique assembly verification problem within the growth-only aTAM with negative interactions is coNP-complete.

Posted on

Nearly Constant Tile Complexity for any Shape in Two-Handed Tile Assembly

Title: Nearly Constant Tile Complexity for any Shape in Two-Handed Tile Assembly

Authors: Robert Schweller, Andrew Winslow, and Tim Wylie

Journal: Algorithmica, 2019

Abstract:

Tile self-assembly is a well-studied theoretical model of geometric computation based on nanoscale DNA-based molecular systems. Here, we study the two-handed tile self-assembly model or 2HAM at general temperatures, in contrast with prior study limited to small constant temperatures, leading to surprising results. We obtain constructions at larger (i.e., hotter) temperatures that disprove prior conjectures and break well-known bounds for low-temperature systems via new methods of temperature-encoded information.

In particular, for all $n \in \mathbb{N}$, we assemble $n \times n$ squares using $O(2^{\log^*{n}})$ tile types, thus breaking the well-known information theoretic lower bound of Rothemund and Winfree. Using this construction, we then show how to use the temperature to encode general shapes and construct them at scale with $O(2^{\log^*{K}})$ tiles, where $K$ denotes the Kolmogorov complexity of the target shape. Following, we refute a long-held conjecture by showing how to use temperature to construct $n \times O(1)$ rectangles using only $O(\log{n}/\log\log{n})$ tile types. We also give two small systems to generate nanorulers of varying length based solely on varying the system temperature.

These results constitute the first real demonstration of the power of high temperature systems for tile assembly in the 2HAM. This leads to several directions for future explorations which we discuss in the conclusion.

Posted on

Full Tilt: Universal Constructors for General Shapes with Uniform External Forces

Title: Full Tilt: Universal Constructors for General Shapes with Uniform External Forces

Authors: Jose Balanza-Martinez, David Caballero, Angel A. Cantu, Luis Angel Garcia, Austin Luchsinger, Rene Reyes, Robert Schweller, and Tim Wylie

Conference: The 30th ACM-SIAM Symposium on Discrete Algorithms (SODA’19), 2019.

Abstract:We investigate the problem of assembling general shapes and patterns in a model in which particles move based on uniform external forces until they encounter an obstacle. In this model, corresponding particles may bond when adjacent with one another. Succinctly, this model considers a 2D grid of “open” and “blocked” spaces, along with a set of slidable polyominoes placed at open locations on the board. The board may be tilted in any of the 4 cardinal directions, causing all slidable polyominoes to move maximally in the specified direction until blocked. By successively applying a sequence of such tilts, along with allowing different polyominoes to stick when adjacent, tilt sequences provide a method to reconfigure an initial board configuration so as to assemble a collection of previous separate polyominoes into a larger shape.

While previous work within this model of assembly has focused on designing a specific board configuration for the assembly of a specific given shape, we propose the problem of designing \emph{universal configurations} that are capable of constructing a large class of shapes and patterns.
For these constructions, we present the notions of \emph{weak} and \emph{strong} universality which indicate the presence of “excess” polyominoes after the shape is constructed. In particular, for given integers $h,w$, we show that there exists a weakly universal configuration with $\mathcal{O}(hw)$ $1 \times 1$ slidable particles that can be reconfigured to build any $h \times w$ patterned rectangle. We then expand this result to show that there exists a weakly universal configuration that can build any $h \times w$-bounded size connected shape. Following these results, which require an admittedly relaxed assembly definition, we go on to show the existence of a strongly universal configuration (no excess particles) which can assemble any shape within a previously studied “Drop” class, while using quadratically less space than previous results.

Finally, we include a study of the complexity of deciding if a particle within a configuration may be relocated to another position, and deciding if a given configuration may be transformed into a second given configuration. In both cases, we show this problem to be PSPACE-complete, even when movable particles are restricted to $1\times 1$ and $2\times 2$ polyominoes that do not stick to one another.

URL:

Bibtex:

Accompanying videos related to the paper

Section 3: Pattern and General Shape Builder

Construction of a Pattern:

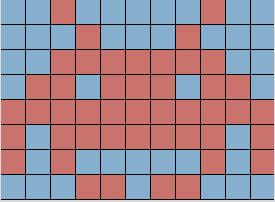
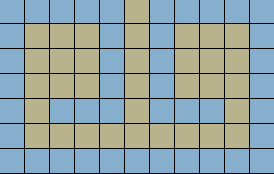
Construction of a Drop Shape:

Construction of a Non-Drop Shape:

Section 4: Drop Shape Builder

Section 5: Relocation Gadget

Example of Correct Traversal Through our Relocation Gadget:

This video shows the correct sequence of tilts to traverse our robot through the gadget.  Note the closed exit/entrance points of our gadgets do not affect this traversal, and are only there to simplify testing

Example of Incorrect State Traversal Attempt Through our Relocation Gadget:

Here we see the robot trying to traverse our gadget while the gadget is not in the correct state to allow the robot to do so. This is only one of the possible sequences, but no sequence of tilts exists that would allow the robot to traverse through the gadget from this position.

Example of Robot Polyomino Becoming Stuck Through Correct State but Incorrect Traversal Sequence:

Here is an example of the importance of our optimal sequence to traverse through the gadget, although there are many ways to traverse, there are also many ways to enter what we call “stuck” configuration. From these configurations there is no sequence of tilts that would allow the robot to leave the gadget.

Section 6: Reconfiguration Gadget

Example of Correct Traversal Through Our Reconfiguration Gadget:

Example of Moving State Tiles to Reconfiguration Ring:

Here we remove all tiles from the inner section of our gadget and into the “reconfiguration ring”. This property of our gadget is what allows us to achieve a global configuration of our gadgets and classify this problem as a reconfiguration problem.

Example of A System of Reconfiguration Gadgets:

This shows a system of reconfiguration gadgets and the robots traversal through the system. At the end of our traversal we move all our state tiles int the reconfiguration ring and achieve a specific configuration of our entire system.

Example of Traversal Sequences that Preserve Initial State Tile Positions:

The videos here show that we can easily traverse gadgets while maintaining the a small set of positions for our state tiles. We know that from these positions we can traverse the gadget with a sequence that will allow us to keep the positions of our red tiles within this set, while not moving any tiles that started in this set into the reconfiguration ring.